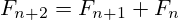Greatest common divisor and Fibonacci numbers

Posted on 2011-07-21

Many people know a very basic fact about Fibonacci numbers:

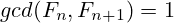
gcd(F_n, F_{n+1}) = 1

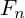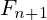In other words: F_n and F_{n+1} are coprime

There is a more generic form:

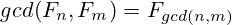
gcd(F_n, F_m) = F_{gcd(n, m)}

The first proposition follows from this, as 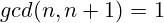gcd(n, n+1) = 1.

Some time ago Johannes and i discovered another fact if n is coprime to 2 and 3:

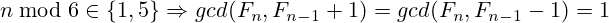
n \bmod{6} \in \{ 1, 5 \} \Rightarrow gcd(F_n, F_{n-1} + 1) = gcd(F_n, F_{n-1} - 1) = 1

Proofing it wasn’t very difficult; just use the identity 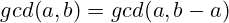gcd(a, b) = gcd(a, b - a) to show the following:

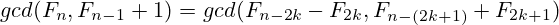
gcd(F_n, F_{n-1} + 1) = gcd(F_{n-2k} - F_{2k}, F_{n-(2k+1)} + F_{2k+1})
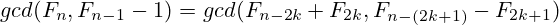
gcd(F_n, F_{n-1} - 1) = gcd(F_{n-2k} + F_{2k}, F_{n-(2k+1)} - F_{2k+1})

Depending on the value of 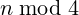n \bmod{4} (only 2 possibilites: 1 and 3) you can choose a value for k which helps to easily simplify at least one sum or difference with the basic identity of the Fibonacci numbers F_{n+2} = F_{n+1} + F_n

Generated using nanoc and bootstrap - Last content change: 2013-08-16 14:47